| 校正雑学 - 反射係数とVSWR |
|
 |
|
■インピーダンスと整合・不整合 (Impedance, matching and mismatching)
高周波の伝送線路において、最も重要かつ基本的な概念がインピーダンスで、伝送線路を高周波電力が伝播するときの電圧と電流の比で表します。ある信号源から、その持っている最大電力を取り出せる条件にすることを「整合」といいます。即ち、信号源と負荷側のインピーダンスが整合した時、最大の電力が取り出せます。両者のインピーダンスが一致しない状態を「不整合」と言います。不整合の状態では、すべての電力が伝送されず、その一部が逆行して戻ってきます。これを「反射波」と言います。
■電圧反射係数 (Reflection coefficient)
進行する波に対し反射して戻ってくる波の電圧振幅の割合をΓ(ガンマ)で表して「電圧反射係数」と呼びます。その値は-1から+1の間になります。負荷側のインピーダンスが0(ゼロ)の時は-1になり、進行波は完全に打ち消されます。いわゆる短絡の状態です。負荷側のインピーダンスが無限大の時+1になり、進行波は2倍の電圧になって戻ってきます。いわゆる開放の状態です。インピーダンスが整合の状態では0(ゼロ)になり、すべての電力が負荷側に吸収されます。
電圧反射係数 Γ = VR / VF --- (1)
ここで、VR=反射波電圧の振幅、VF=進行波電圧の振幅
電圧反射係数Γは大きさと位相の2つの情報を含んでいる複素数ですが、その絶対値|Γ|と後述するVSWRとの間には次の関係があります。
電圧反射係数の絶対値|Γ| = (VSWR-1) / (VSWR +1) --- (2)
インピーダンスで表すと
電圧反射係数 Γ = (ZX - Z0) / (ZX + Z0) --- (3)
ここで、ZX=被測定物のインピーダンス(Ω)
Z0= 測定回路の特性インピーダンス(Ω) ・・・一般には50Ω
また、リターンロス(dB値)から電圧反射係数の絶対値を求めるには次の式を用います。
電圧反射係数の絶対値 |Γ| = 10(リターンロス/-20) --- (4)
■電圧定在波比 (Voltage standing wave ratio - VSWR)
進行波と反射波の干渉から生まれる、伝送線路上の波(定在波)の最大電圧の絶対値VMAXを最小電圧の絶対値VMINで割った値で、無反射(完全整合)の場合は1になります。なお、VSWRの値は大きさのみの情報であり位相情報は含みません。
VSWR = VMAX / VMIN --- (5)
VSWR = (1+|Γ|) / (1-|Γ|) --- (6)
ここで、Γ=電圧反射係数
■リターンロス (Return loss)
線路の特定の点において、入射波が反射して元の方向に戻る時、どれだけ減衰するかを表すパラメータです。100%反射の時はゼロとなり、減衰無しに全てが反射波になります。無反射の時は無限大となり、無損失で反射波は存在しないということになります。
リターンロス(dB) = -10 x LOG(PR/PF) --- (7)
リターンロス(dB) = -20 x LOG|Γ| --- (8)
ここで、PR=反射電力、PF=進行電力、Γ=電圧反射係数
■電圧反射係数Γから被測定物のインピーダンスZxの求め方
測定回路の特性インピーダンスが50Ωの場合
(How to calculate an impedance from value of reflection coefficient)
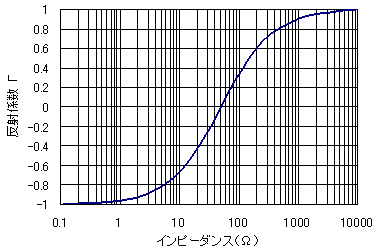
前述の(3)式から、測定される電圧反射係数Γは、被測定物のインピーダンスZxに応じて、-1から+1まで変化します。その様子を図1に示します。即ち、反射係数が+1の場合のインピーダンスは無限大(開放状態)、-1の場合のインピーダンスはゼロ(短絡状態)になります。
|
|
|
 |
|
図1 反射係数とインピーダンスの関係
注)Zxが抵抗性(Rx+j0)の場合 |
被測定物の反射係数Γ(大きさと位相情報の2つ)が測定できれば、その値を下式に代入することで、被測定物のインピーダンスZxを求めることができます。なお、VSWRの値は位相情報を含んでいない為、リアクタンス成分が無視できない場合は、VSWRの値から正確なインピーダンスを計算することはできません。
Zx = ((1+Γ)/(1-Γ)) x 50 --- (9)
例1)校正の結果、反射係数Γ = +0.0002を得た場合
Zx = ((1+(+0.0002))/(1-(+0.0002))) x 50 = 50.0200Ω
例2)校正の結果、反射係数Γ = -0.0002を得た場合
Zx = ((1+(-0.0002))/(1-(-0.0002))) x 50 = 49.9800Ω |
|
|